It seems the information you shared about "My text" primarily discusses medical degrees like DO and MD, and the difference between "do" and "due." That's quite interesting for someone exploring medical careers or grammar, but it doesn't really connect with the topic of "how to do area of a triangle." So, for this blog post, we'll focus entirely on the geometry part, helping you figure out triangle areas without bringing in medical definitions or grammar rules.

Ever wondered how to find the space a triangle takes up? Maybe you're working on a school project, perhaps you're just curious about shapes, or you might be trying to figure out how much paint you need for a triangular wall. Whatever your reason, figuring out how to do area of a triangle is a pretty useful skill, and it's actually much simpler than you might think. We're going to walk through it step-by-step, making sure you get a good grasp of this basic geometry idea.

You know, triangles are everywhere, aren't they? From roof gables on houses to slices of pizza, or even some road signs, they pop up all over the place. Knowing how to measure their inner space, which we call the area, can certainly help in many everyday situations. It’s a core concept in math, and honestly, once you see the formula, it just clicks.

So, get ready to make friends with a really straightforward formula. We'll explore what you need to know, how to put it all together, and even look at some common questions people have. It’s a bit like learning a simple recipe; you gather your ingredients, follow the steps, and then you have your answer. You’ll be a pro at this in no time, that’s for sure.

• Hispanic Heritage Month
• Shrinking Tv

Table of Contents

• What's the Big Deal About Triangle Area?
• The Simple Secret: The Formula
  • What is "Base"?
  • What is "Height"?
• Step-by-Step: How to Do Area of a Triangle
  • Example 1: A Basic Triangle
  • Example 2: A Right Triangle
  • Example 3: Finding a Missing Part
• Units of Measurement: Very Important!
• Common Things to Watch Out For
• Frequently Asked Questions

What's the Big Deal About Triangle Area?

Well, to be honest, knowing how to do area of a triangle is pretty fundamental in geometry. It helps you understand how much flat space a two-dimensional shape occupies. This isn't just for math class; it's quite practical, like when you're trying to figure out how much material you need for something shaped like a triangle, or maybe even planning a garden plot. It’s a skill that, once learned, you’ll find yourself using in various unexpected ways, too it's almost.

The main audience for this kind of information is usually students, perhaps parents helping with homework, or anyone who just needs a quick refresher on basic geometry. Their interest is typically in getting a clear, straightforward explanation without a lot of confusing jargon. People often feel a bit stuck when they see a math problem, so a simple guide can really help them feel more confident, you know.

The biggest pain point for many is probably remembering the exact formula or understanding what "base" and "height" actually mean in the context of a triangle. That's why we're going to break it down into really small, easy-to-digest pieces. The search intent here is definitely informational; people want to learn, not buy anything. They're looking for answers to "how-to" questions, and that's what we're providing, basically.

• Supergirl
• Christopher Nolan Tenet

The Simple Secret: The Formula

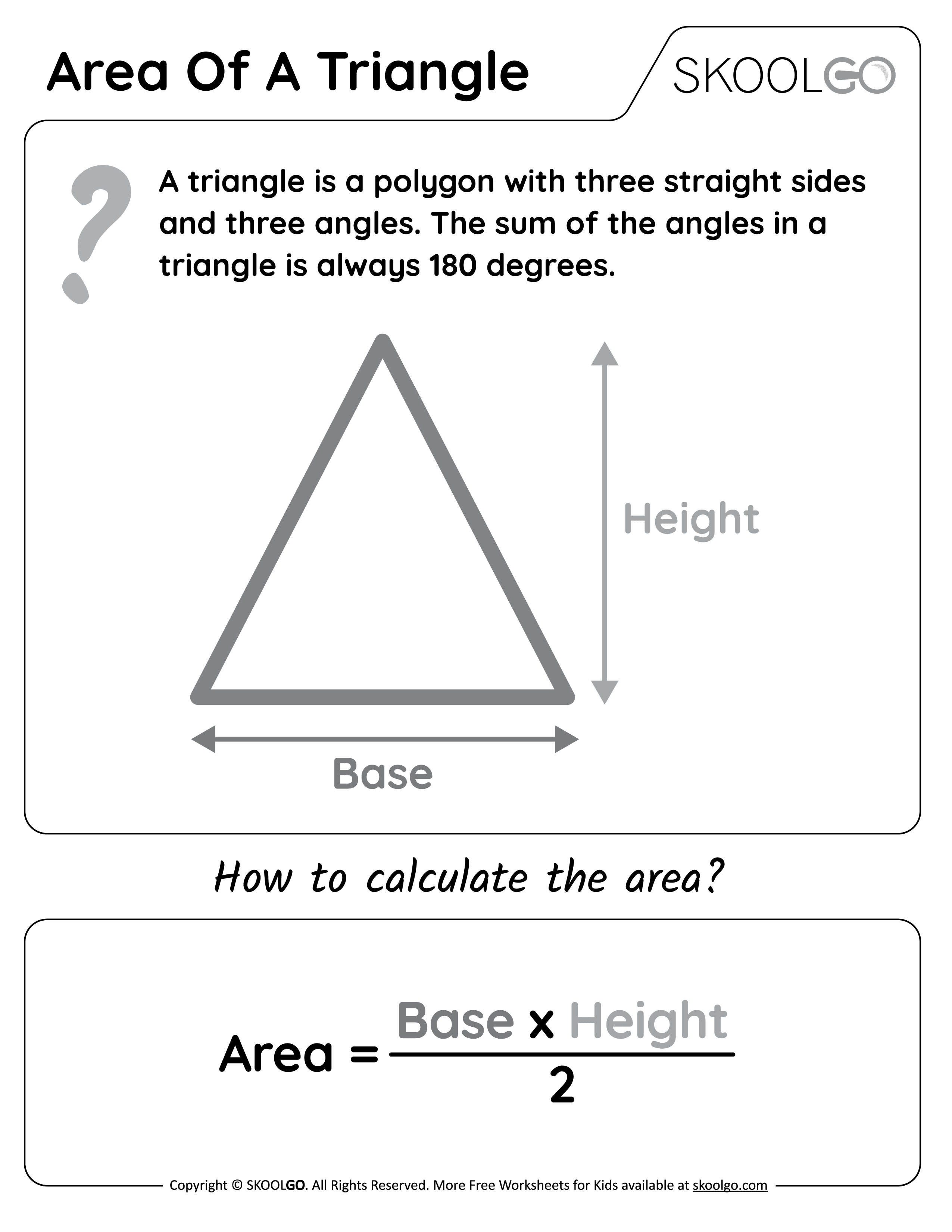
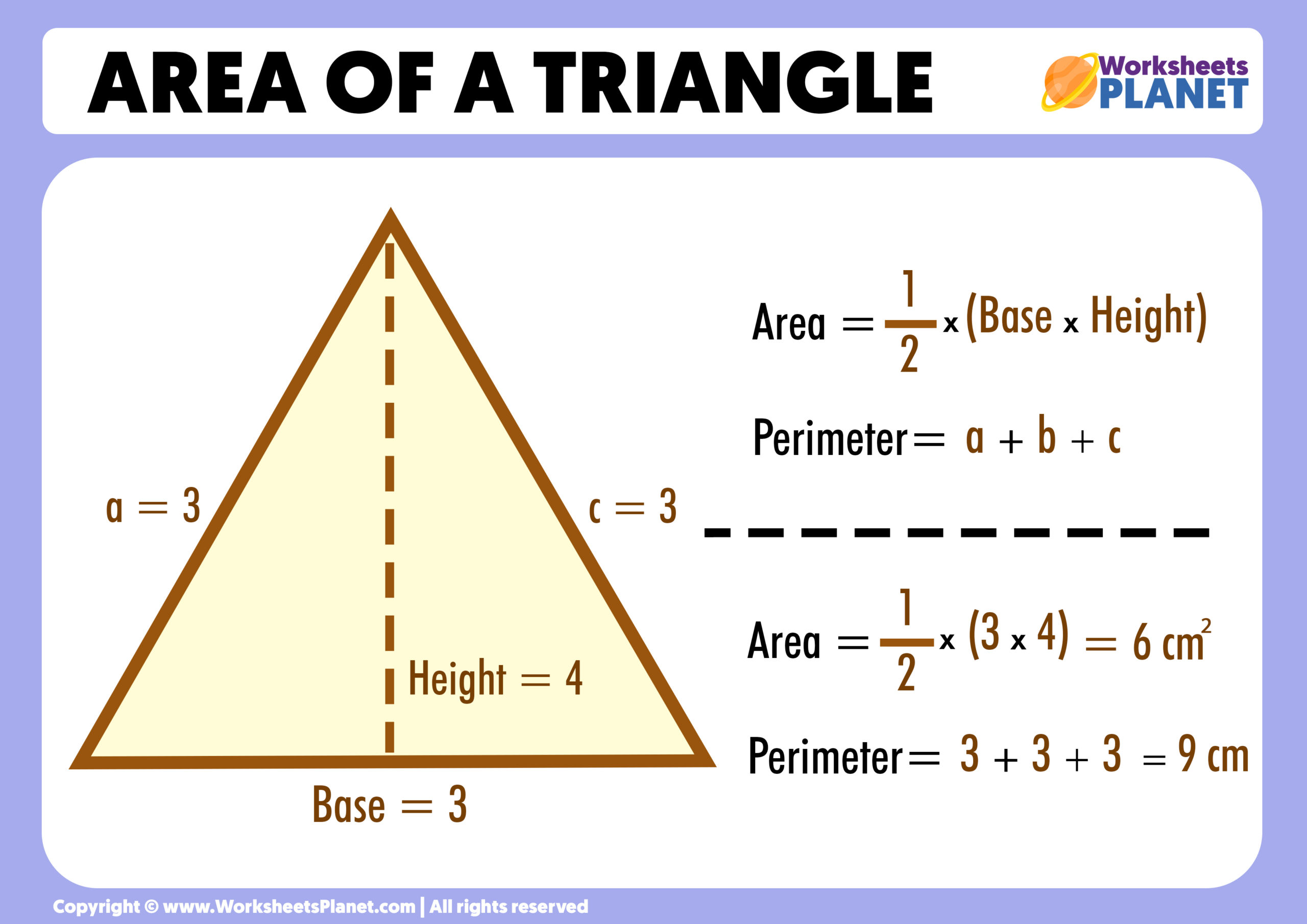
Alright, let's get right to the heart of it. The formula for how to do area of a triangle is one of the most famous and widely used in geometry. It's really simple to remember, and you'll be surprised how often you might use it. The formula goes like this: Area = (1/2) × Base × Height. Or, if you prefer, Area = (Base × Height) / 2. They mean the same thing, just expressed a little differently, as a matter of fact.

This formula works for every single type of triangle, whether it's pointy, wide, or has a right angle. That's what makes it so powerful. You just need two key pieces of information: the length of its base and its perpendicular height. Once you have those, the rest is just simple multiplication and division, you know?

What is "Base"?

When we talk about the "base" of a triangle, we're referring to one of its sides. You can actually choose any side of the triangle to be the base. It's usually the side that the triangle appears to be "sitting on," but it doesn't have to be. For example, if you turn a triangle on its side, that side can become the new base. It’s a bit flexible in that way, you see.

The length of this chosen side is what you'll plug into your formula. It's a straight measurement, just like measuring any line segment. Make sure you're consistent with your units of measurement, too. If your base is in centimeters, your height should also be in centimeters, for instance.

What is "Height"?

Now, the "height" is where some people get a little mixed up, but it's really not hard. The height of a triangle is the perpendicular distance from the base you chose to the opposite corner (or vertex). "Perpendicular" just means it forms a perfect right angle (90 degrees) with the base. It's like dropping a straight line from the highest point of the triangle down to the base, forming a neat square corner, so.

Sometimes, this height line might fall outside the triangle itself, especially with triangles that lean over a lot (we call those obtuse triangles). That's perfectly fine. You still measure that straight-down distance from the top point to the line where the base extends. It's always a straight shot down, very, very precise.

Step-by-Step: How to Do Area of a Triangle

Okay, let's put it all together with some real-world-ish examples. The process is always the same, no matter what your triangle looks like. You identify the base, you find the height, you multiply them, and then you cut that number in half. It’s pretty straightforward, really.

Example 1: A Basic Triangle

Imagine you have a triangle. Let's say its base measures 10 units long. And let's say the height, measured straight up from that base to the opposite corner, is 6 units. How would you figure out its area? Well, you just follow the formula, you know?

1. Write down the formula: Area = (Base × Height) / 2
2. Plug in your numbers: Base = 10, Height = 6. So, Area = (10 × 6) / 2
3. Do the multiplication: 10 × 6 equals 60.
4. Do the division: 60 divided by 2 equals 30.
5. State your answer with units: The area is 30 square units. That’s it! Pretty simple, right?

This is the most common scenario you'll encounter. It’s about recognizing the parts and then applying the math. And, you know, practicing a few times really helps it stick in your mind, too.

Example 2: A Right Triangle

Right triangles are a special case, and they can sometimes make finding the height even easier. A right triangle has one angle that's exactly 90 degrees, like the corner of a square. The two sides that form this right angle are already perpendicular to each other. So, one of those sides can be your base, and the other side that forms the right angle will automatically be your height. It's very convenient, actually.

Let's say you have a right triangle. One side forming the right angle is 8 meters long, and the other side forming the right angle is 5 meters long. How do you find its area? You can pick either of those sides as the base, and the other will be the height. Let's say Base = 8 meters and Height = 5 meters, basically.

1. Formula: Area = (Base × Height) / 2
2. Plug in: Area = (8 × 5) / 2
3. Multiply: 8 × 5 equals 40.
4. Divide: 40 divided by 2 equals 20.
5. Answer: The area is 20 square meters. See how easy that was? It's really just the same process, just with a little shortcut for identifying the base and height.

Example 3: Finding a Missing Part

Sometimes, you might already know the area of a triangle, and perhaps one of the other measurements, like the base, but you need to find the height. This is just working the formula backward, which is pretty neat. Let's say the area of a triangle is 40 square centimeters, and its base is 10 centimeters. What's the height? This is where a little algebra comes into play, but it’s still simple, honestly.

1. Start with the formula: Area = (Base × Height) / 2
2. Plug in what you know: 40 = (10 × Height) / 2
3. Get rid of the division by 2: Multiply both sides of the equation by 2. So, 40 × 2 = 10 × Height, which means 80 = 10 × Height.
4. Isolate the Height: To find Height, divide both sides by 10. So, 80 / 10 = Height.
5. Calculate: Height = 8 centimeters.

This shows how versatile the formula is. You can use it to find any of the three main components if you have the other two. It’s like a little puzzle you can solve, and it’s quite satisfying when you get the answer, too.

Units of Measurement: Very Important!

When you're figuring out how to do area of a triangle, the units you use are incredibly important. If your base is measured in meters and your height is in meters, then your area will be in "square meters" (m²). If they're in inches, your area will be in "square inches" (in²). It's always "square" units for area, because you're measuring a two-dimensional space. This is a common point where people sometimes make a small mistake, you know, forgetting the "square" part.

Always make sure your base and height are in the same units before you do any calculations. If one is in centimeters and the other is in meters, you'll need to convert one of them so they match. For instance, you might change meters to centimeters, or vice versa. Consistency is really the key to getting the correct answer, that's for sure.

Common Things to Watch Out For

Even though the formula for how to do area of a triangle is simple, there are a couple of things people sometimes trip over. One big one is confusing the height with a slanted side of the triangle. Remember, the height must always be perpendicular to the base, forming that perfect right angle. It's not just any side that goes up to the top, so.

Another thing is making sure you actually divide by two at the end. It's easy to just multiply the base and height and forget that final step. Think of it this way: a triangle is basically half of a rectangle or a parallelogram with the same base and height. That's why you divide by two, actually. It's a pretty neat way to visualize it, too.

And then there's the unit consistency we just talked about. Double-check your units before you start. It’s a small detail, but it can make a huge difference in your final answer. A quick check can save you from a lot of head-scratching later on, you know?

For more general math help and to perhaps explore other geometric shapes, you might find resources like Khan Academy very helpful. They have tons of lessons that can help you understand all sorts of math concepts, from basic arithmetic to more advanced topics. It’s a great place to learn more about things like this, basically.

And hey, if you want to learn more about shapes and measurements on our site, or maybe even explore some other math topics, we have plenty of articles that could be just what you're looking for. There's always more to learn, and we try to make it as clear as possible, like your own personal guide.

Frequently Asked Questions

What is the formula for the area of a triangle?

The formula for the area of a triangle is quite straightforward: Area = (1/2) × Base × Height. You can also write it as Area = (Base × Height) / 2. Both ways give you the same result. You just need to find the length of one side (your base) and the perpendicular distance from that base to the opposite corner (your height), and then do a little multiplication and division, that's it.

How do you find the area of a triangle without the height?

Finding the area of a triangle without knowing its height is a bit more involved, but it's certainly possible. One common method uses something called Heron's formula, which works if you know the lengths of all three sides of the triangle. It involves calculating something called the "semi-perimeter" first, and then plugging that into a slightly more complex formula. This approach often comes up in higher-level geometry, so it’s not usually the first method you learn for how to do area of a triangle. For this particular discussion, we're sticking to the base and height method, which is the most fundamental way to approach it, basically.

What are the units for area?

The units for area are always "square units." So, if your measurements for base and height are in centimeters, the area will be in square centimeters (cm²). If they are in meters, the area will be in square meters (m²). This is because area measures a two-dimensional space, almost like counting how many little squares would fit inside the shape. It's a pretty important detail to remember when you write down your final answer, you know, to make sure it's completely accurate.